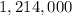Question

The mosquito population of a national park was 800,000 in 2003. If the population grew at a rate of 8.7% per year, approximately how many mosquitoes would havebeen in the park in 2008

Answer 1

Let P be the initial population of mosquitoes for a given year. Let k be the percentual increase of the population over a year.

To calculate the population after a year, first calculate the increase by multiplying k times P:

`\text{Increase}=k\cdot P`

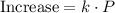
Add the increase to the initial population to know the population after a year:

`\begin{gathered} \text{Population after a year }=\text{ Increase + initial population} \\ =P+kP \\ =(1+k)\cdot P \end{gathered}`

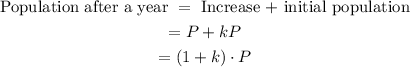
Therefore, to calculate the population after a year, we have to multiply the initial population by (1+k).

To calculate the population after two years, take (1+k)P as the new initial population:

`\begin{gathered} \text{Population after 2 years }=(1+k)\cdot(1+k)P \\ =(1+k)^2\cdot P \end{gathered}`

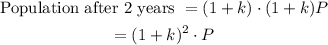
By analogy, after n years, the population will be equal to:

`(1+k)^n\cdot P`

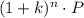
Since 5 years pass from 2003 to 2008, the initial population was 800,000 and the yearly percentual increase is 8.7%, then n=5, P=800,000 and k=8.7/100. Substitute in the formula to know the population of mosquitoes in 2008:

`\begin{gathered} (1+(8.7)/(100))^5\cdot800,000 \\ =(1+0.087)^5\cdot800,000 \\ =(1.087)^5\cdot800,000 \\ =1.517566463\cdot800,000 \\ =1,214,053.17 \end{gathered}`

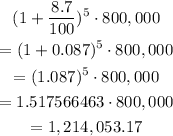
Therefore, the population of mosquitoes in the park in 2008 will be approximately (to the nearest tousand):

`1,214,000`