Question

Plsssssss help its easy i just not good at this particular thing

Answer 1

Inequality:

x + 15.4 ≤ 18.7

Solution:

x≤ 3.3

1) Considering that we have the measures of each side, and the sum of all sides (Perimeter) we can write out the following:

`\begin{gathered} 4.9+4.1+x+6.4\leq18.7 \\ \end{gathered}`

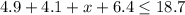
2) Let's now add them all up to get the possible values of x:

`\begin{gathered} 4.9+4.1+x+6.4\leq18.7 \\ 9+x+6.4\leq18.7 \\ x+15.4\leq18.7 \\ x+15.4-15.4\leq18.7-15.4 \\ x\leq3.3 \end{gathered}`

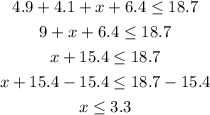
Note that we have isolated x on one side, by subtracting 15.4 from both sides. So the missing side must be lesser than or equal to 3.3 units

3) Hence, the answer is:

Inequality:

x + 15.4 ≤ 18.7

Solution:

x≤ 3.3