Answer:
• Vertex Form: f(x)=(x+5)²-7
,
• Vertex: (-5, -7)
,
• Axis of symmetry: x=-5
,
• Graph: See below
Explanation:
Given the function:
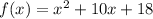
Wo want t wrerite the function in the vertex form y=a(x-h)².
In order to do this, complete the square for x.

The vertex form of the function is:

The vertex of the function:
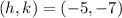
The axis of symmetry is the x-value at the vertex, therefore, the axis of symmetry is:

Graph
In odert to graph th function, find two otherpoints ton the graph.
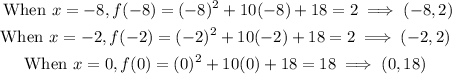
Plot the vertex, (-5,-7) and the poins (-8,2), (-2,2) and (0,18).
The graph of f(x) is attached below: