Question

Write each function in vertex form identify the vertex and axis of symmetry, then graphf(x)=x^2+10x+18=

Answer 1

• Vertex Form: f(x)=(x+5)²-7

,

• Vertex: (-5, -7)

,

• Axis of symmetry: x=-5

,

• Graph: See below

Explanation:

Given the function:

`f(x)=x^2+10x+18`

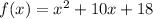
Wo want t wrerite the function in the vertex form y=a(x-h)².

In order to do this, complete the square for x.

`\begin{gathered} f(x)=x^2+10x+18 \\ \text{Divide the coefficient of x by 2, square it and add it to both sides.} \\ f(x)+5^2=x^2+10x+5^2+18 \\ f(x)+25=(x+5)^2+18 \\ \text{ Subtract 25 from both sides} \\ f(x)+25-25=(x+5)^2+18-25 \\ f(x)=(x+5)^2-7 \end{gathered}`

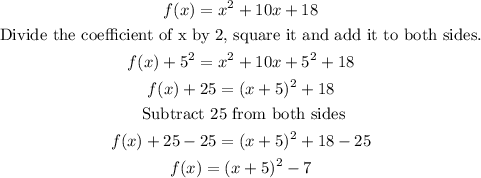
The vertex form of the function is:

`f(x)=(x+5)^2-7`

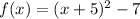
The vertex of the function:

`\left(h,k\right)=(-5,-7)`

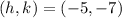
The axis of symmetry is the x-value at the vertex, therefore, the axis of symmetry is:

`x=-5`

Graph

In odert to graph th function, find two otherpoints ton the graph.

`\begin{gathered} \text{ When }x=-8,f(-8)=(-8)^2+10(-8)+18=2\implies(-8,2) \\ \text{When }x=-2,f(-2)=(-2)^2+10(-2)+18=2\implies(-2,2) \\ \text{When }x=0,f(0)=(0)^2+10(0)+18=18\implies(0,18) \end{gathered}`

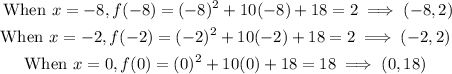
Plot the vertex, (-5,-7) and the poins (-8,2), (-2,2) and (0,18).

The graph of f(x) is attached below: