Question

Which accurately describes the equation of y=-3x^2 + 12x - 9? *Mark only one oval.vertex at (2, 3); passes through (0, 1)vertex at (2, 3); passes through (1, 0)vertex at (3, 2); passes through (0, 1)O vertex at (3, 2

Answer 1

Given:

`y=-3x^2+12x-9`

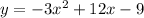
Required:

We need to find the vertex and the point lies on the given parabola.

Step-by-step explanation:

The given equation is of the form.

`y=ax^2+bx+c`

where a =-3, b =12 and c =-9.

Consider the formula to find the x-coordinate of the vertex.

`x=-(b)/(2a)`

Substitute a =-3 and b =12 in the formula.

`x=-(12)/(2(-3))`
`x=-(12)/(-6)`
`x=2`

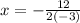
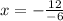
Substitute x =2 in the given equation to find the y-coordinate of the vertex.

`y=-3(2)^2+12(2)-9`
`y=-12+24-9`
`y=3`

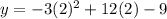
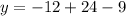
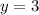
The vertex is (2,3).

Substitute x =0 in the given equation.

`y=-3(0)^2+12(0)-9`
`y=-9`

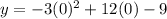
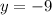
The point is (0,-9).

Substitute x =1 in the given equation.

`y=-3(1)^2+12(1)-9`
`y=-3+12-9`
`y=0`

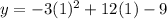
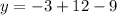
The point is (1,0).

Final answer:

Vertec at (2,3) and passes through (1,0).