Question

Given the coordinates, Complete the translation (,)→(+2,−2) ( x , y ) → ( x + 2 , y − 2 ) .

Answer 1

The transformation given tells us to add 2 to the x-coordinate (the first in the ordered pair x,y) and subtract 2 from the y-coordinate (the second in the ordered pair x,y).

That is what (x, y) -> (x + 2, y - 2) means.

Then, we can now easily work on each of the 4 coordinates given:

For C:

`C=(-5,-1)`

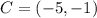
The x-coordinate is -5 and the y coordinate is -1. As stated at the beginning, we need to add 2 to the x-coordinate to form the new x-coordinate (the one of C'). That will be -5 + 2 = -3.

Subtracting 2 from the y-coordinate as instructed for the y-coordinate of C', we have -1 - 2 = -3.

Then:

`C(-5,-1)\rightarrow C´(-3,-3)`

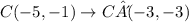
For the other coordinates we just need to follow the same logic:

`D(-4,3)\rightarrow D´(-4+2,3-2)\rightarrow D´(-2,1)`
`E(-3,2)\rightarrow E´(-3+2,2-2)\rightarrow E´(-1,0)`
`F(-2,0)\rightarrow F´(-2+2,0-2)\rightarrow F´(0,-2)`

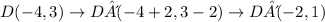
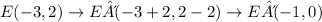
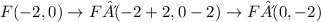
Then, the blanks should be filled as follows:

C'(-3, -3)

D'(-2, 1)

E'(-1, 0)

F'(0, -2)