We will assume that we have the next system of equations:
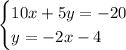
Now, since we have to use the substitution method, we need to write the equivalent expression of one of the unknown variables in one of the given equations.
We can see that the unknown variable, y, is given explicitly in the form:
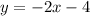
Then, we can substitute this equation in the first one as follows:
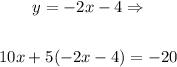
And now, we have to solve the resulting expression by using the distributive property, and then simplifying the result as follows:
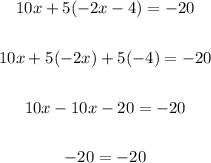
Since we ended with this result, we can say that we have an infinite number of solutions, and if we need to express the solutions in terms of x, we can write that the solutions are given, then, by:
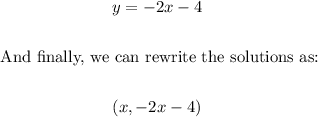
In summary, the solution for this system can be written - in terms of x - as follows: (x, -2x-4).