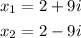Question

Solve: x² - 4x + 85=0 A. {7+3i, 7 - 3i B. {2+9i, 2 – 91 c. {3+ 71,3 - 7i O D. {2+191,2 - 1911

Answer 1

We are given the following equation:

`x^(2)-4x+85=0`

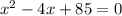
To solve for "x" we will use the quadratic formula, which is:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where the values of "a", "b" and "c" are the coefficients of the equation:

`ax^2+bx+c`

Therefore, in this case, we have:

`\begin{gathered} a=1 \\ b=-4 \\ c=85 \end{gathered}`

Replacing in the quadratic formula:

`x=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(85)}}{2(1)}`

Solving the operations inside the radical:

`x=\frac{-(-4)\pm\sqrt[]{-324}}{2}`

Now we divide the number inside the radical a the product of -1 and 324:

`x=\frac{-(-4)\pm\sqrt[]{(-1)(324)}}{2}`

Now we divide the square root:

`x=\frac{-(-4)\pm\sqrt[]{(-1)}\sqrt[]{324}}{2}`

The square root of -1 is the imaginary unit "i". Therefore, solving the square roots we get:

`x=(-(-4)\pm18i)/(2)`

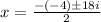
Now we separate the fraction:

`x=(-(-4))/(2)\pm(18i)/(2)`

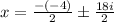
Solving the operations:

`x=2\pm9i`

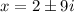
Therefore, the solutions of the equation are:

`\begin{gathered} x_1=2+9i \\ x_2=2-9i \end{gathered}`