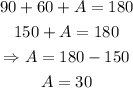Question

Find the quantities in the photo find a, B, and A.Type in integral or decimal rounded to the nearest TENTH as needed.

Answer 1

`\begin{gathered} (a)a=9.2 \\ (b)b=18.5 \\ (c)A=30\degree \end{gathered}`

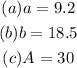
Step-by-step explanation

(a) To find the value of a, we have to apply trigonometric ratios, SOHCAHTOA, for tangent for right triangles:

`\tan 60=(opposite)/(adjacent)`

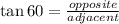
Therefore, we have that:

`\begin{gathered} \tan 60=(16)/(a) \\ \Rightarrow a=(16)/(\tan 60) \\ a=9.2 \end{gathered}`

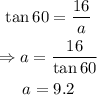
(b) To find the value of b, we have to apply trigonometric ratios, SOHCAHTOA, for sine for right triangles:

`\sin 60=\frac{\text{opposite}}{\text{hypotenuse}}`

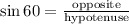
Therefore, we have that:

`\begin{gathered} \sin 60=(16)/(b) \\ \Rightarrow b=(16)/(\sin 60) \\ b=18.5 \end{gathered}`

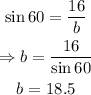
(c) To find the measure of A, apply the total angle in a triangle.

The sum of angles in a triangle is 180 degrees. This implies that:

`\begin{gathered} 90\degree+60\degree+A=180\degree \\ 150\degree+A=180 \\ \Rightarrow A=180\degree-150\degree \\ A=30\degree \end{gathered}`