SOLUTION
Steps1: Define a parameter for the unknow
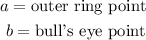
Step2: Write out the equation for Helen
Since Helen landed 3arrows on the outer ring and 1 on the bull's eye and have a total of 174, the equation becomes
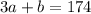
Step3: Wite out the equation for Jordan
Since Jordan Landed 3arrows on outer ring and 4arrows in the bull's eye with a total point of 444, the equation becomes
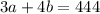
Step4: Solve the system of equation with elimination method
To solve the equation, we label them eliminate the variables separately
hence
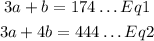
Subtract Eq1 from Eq2 (Eq2-Eq1) to eliminate the variable a.
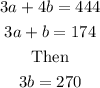
From the equation in the last line above divide both sides by 3, we have
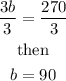
To eliminate the variable b, Multiply Eq1 by 4 and subtract from Eq 2, we have

From the equation in the last line above, divide both sides by 9, we obtain
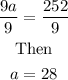
Hence
a=28,b=90.
Therefore
The outer ring worth 28 point
The bull's eye worth 90 point