Question

I’m confused on how to find sequences that are convergent?

Answer 1

The Solution:

A geometric sequence is said to converge if the value of the modulus of r is less than one, that is, when |r| < 1, the series converges. But when |r| ≥ 1, the series/sequence diverges.

Clearly, we have that:

`\begin{gathered} \text{ r=3 does not converge } \\ \text{ So, option A does not converge.} \end{gathered}`

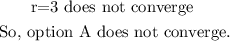
[Option C] converges since

`|r|=(3)/(5)<1`

Similarly,

[Option E] converges since

`|r|=-(1)/(6)<1`

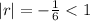
Therefore, the correct answer is [option C and E]