Solution:
Given:
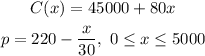
The revenue is given by;
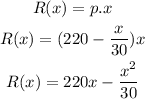
Question A:
The profit is the difference between the revenue and the cost.
Hence,

To get the maximum profit, we differentiate the profit function.
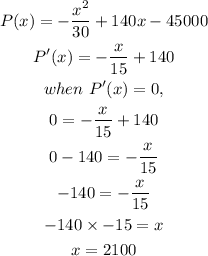
Therefore, the production level that results in maximum profit is x = 2100
Question B:
The price for each drill to maximize profit is;
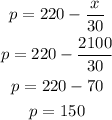
Therefore, the price the company should charge for each drill is 150