Answer:
The magnification = 0.52
Step-by-step explanation:
Power, P = -4.10D
Object distance, u = 22.5 cm
Focal length, f = 100/power
f = 100/-4.10
f = -24.39 cm
Using the formula below, calculate the image distance (v)
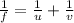
Substitute u = 22.5, f = -24.39, and solve for v
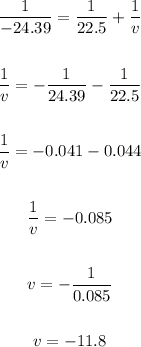
The magnification, M = |v/u|
M = |-11.8/22.5|
M = |-0.52|
M = 0.52
The magnification = 0.52