Given equation is

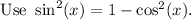
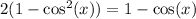

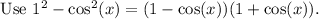
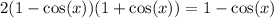
Cancel out the common term on both sides, we get
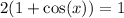
Dividing both sides by 2, we get
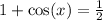
Subtracting 1 from both sides, we get
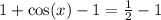
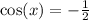
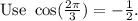
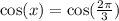
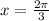
Hence the exact value of x is
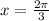
The exact values of all angles in the interval [0, pi] that satisfy the given equation is 2pi/3.