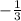Question

Consider the following three points.(-5,2), (0, 6), (6,4)Step 2 of 3: Find the slope of the line between the second and third points.

Answer 1

Given the three points to be

`(-5,2),\text{ (0, 6), (6,4)}`

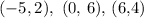
Let A, B, C respectively represent the three points such that

`\begin{gathered} A(-5,2), \\ B(0,\text{ 6),} \\ C(6,\text{ 4)} \end{gathered}`

The slope m of a line between any two points is given as

`\begin{gathered} m\text{ = }(y_2-y_1)/(x_2-x_1)\text{ ----- equation 1} \\ \text{where } \\ m\text{ }\Rightarrow slope\text{ of the line} \\ (x_(1,)y_1)\Rightarrow coordinates\text{ of one point} \\ (x_2,y_2)\Rightarrow coordinates\text{ of the other point} \end{gathered}`

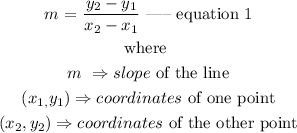
The slope of the line between the second and third points is evaluated as

`\begin{gathered} \text{second point}\Rightarrow B(0,6)\text{ = }(x_1,y_1) \\ \text{third point}\Rightarrow C(6,4)\text{ = }(x_2,y_2) \\ \text{Substitute the above values into equation 1} \\ thus, \\ m\text{ = }(4-6)/(6-0)\text{ =}\frac{\text{-2}}{6} \\ \Rightarrow m=-(1)/(3) \\ \\ \end{gathered}`

Hence, the slope between the second and third points is evaluated to be

`-(1)/(3)`