Solution:
We are given an irregular pentagon. To calculate the area, we will have to break the pentagon into component shapes
We can break the pentagon into a trapezium and a triangle
The dimensions of the trapezium are :
1st base = 3 units
2nd base = 4 units
Height = 3 units
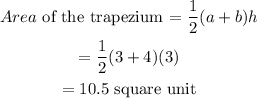
The dimensions of the triangle are:
Base= 4 units
Height=2 units
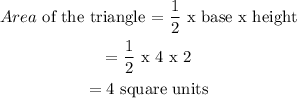
Area of the polygon = area of trapezium + area of triangle
= 10.5 square unit + 4 square unit = 14.5 square unit
The answer is 14.5 square units