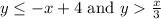SOLUTION
To get the system of equation, we have to get the equation of both lines
For the first line, that is the thick line, let us get the slope of the line
Let's take two points on the line (0, 4) and (4, 0)
We have the slope as
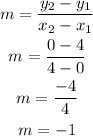
So, the slope of the first line is - 1,
Now equation of a line in slope-intercept form is given as
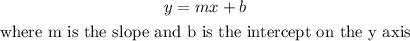
So, since the line cuts the y-axis at 4, the y-intercept is 4
So, the equation of the line is
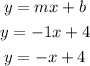
But since, it is an inequality, it is a thick line and the shaded part downward to the left, the equation of this line becomes
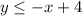
Now, for the second line, this line passes through the origin, so the y-intercept is 0,
So, the equation of the line should be

But since this line is a broken line (less than/greater than) and the shaded part is above, to the right (greater than)
The equation of the line becomes
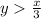
Hence, our answer is the system of equations for the shaded portion of the line is