Since the function is linear, we know that it is a line.
Let's use points (2,1) and (4,4) to calculate the slope:
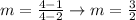
We can use this slope, point (2,1) and the slope-intercept form to find an equation, as following:
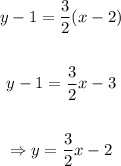
Thereby, our function would be:
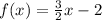
To fill the table,
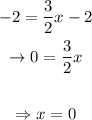
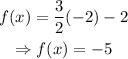
The complete table would be: