Question

Complete the table, given that the function described by the data is linear.

Answer 1

Since the function is linear, we know that it is a line.

Let's use points (2,1) and (4,4) to calculate the slope:

`m=(4-1)/(4-2)\rightarrow m=(3)/(2)`

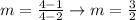
We can use this slope, point (2,1) and the slope-intercept form to find an equation, as following:

`\begin{gathered} y-1=(3)/(2)(x-2) \\ \\ y-1=(3)/(2)x-3 \\ \\ \Rightarrow y=(3)/(2)x-2 \end{gathered}`

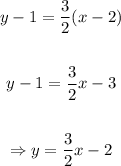
Thereby, our function would be:

`f(x)=(3)/(2)x-2`

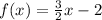
To fill the table,

`\begin{gathered} -2=(3)/(2)x-2 \\ \rightarrow0=(3)/(2)x \\ \\ \Rightarrow x=0 \end{gathered}`
`\begin{gathered} f(x)=(3)/(2)(-2)-2 \\ \Rightarrow f(x)=-5 \end{gathered}`

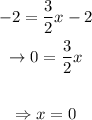
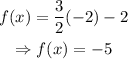
The complete table would be: