In any quadratic expression :

We can factor it by :
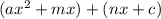
where m and n can be obtained using the ac method.
m and n are the factors of the product of a and c which has a sum of b
From the problem, we have :
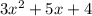
a = 3, b = 5 and c = 4
The product of a and c is 3 x 4 = 12
We need to think of factors of 12 which has a sum of b = 5 for m and n.
The factors of 12 are :
1 x 12
2 x 6
3 x 4
and the sum of any pair is NOT equal to 5.
Therefore, the given quadratic expression is NOT Factorable
ANSWER :
Not factorable