Question 25.
Given the function:
f(x) = 2x + 1
Let's find the inverse of the function.'
Rewrite f(x) for y:
y = 2x + 1
Interchange the variables:
x = 2y + 1
Now, solve the equation for y:
x =2y + 1
Subtract 1 from both sides:
x - 1 = 2y + 1 - 1
x - 1 =2y
Divide all terms by 2:
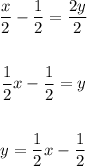
The inverse of the function is:
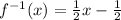
Let's graph both the inverse and parent functions using two lines each.
For the paent function
y = 2x + 1
When x = 1:
y = 2(1) + 1
y = 3
When x = 2:
y = 2(2) + 1
y = 5
We have the points:
(1, 3) and (2, 5)
For the inverse function:
When x = 1
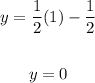
When x = 2:
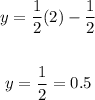
We have the points:
(1, 0) and (2, 0.5)
The graph is attached below
The red line represents the parent function.
The blue line represents the inverse.
The green dotted line represents the line (y = x).