First, notice that we have the results of 45 surveys, then, if A is the event {the customer is pleased} and B is the evente {the customer purchased a Toes Knows shoes}, then their probabilities are:

then, the probability that both A and B occur is:
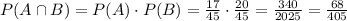
therefore, the probability that a random selected customer is pleased and purchased a Toes Knows shoe is 68/405