We are given a rhombus figure.
Recall that the consecutive angles in a rhombus add up to 180°
This means that the sum of m∠P and m∠S must be equal to 180°
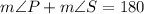
Let us substitute the given values into the above equation and solve for b
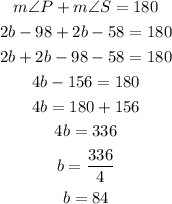
So, the value of b is 84
Now we can find the angle m∠P
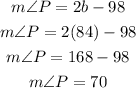
Therefore, the value of m∠P is 70°