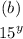Step-by-step explanation:
Given;
We are given the expression shown below;
![(9^(-2))(3^(11))(\sqrt[3]{27})](https://img.qammunity.org/2023/formulas/mathematics/college/grbus0eo7ygl8qxsesh7kqe6s0luttjw0i.png)
Required;
We are required to express this as a single power.
Step-by-step solution;
To do this we would begin by applying some basic rules of exponents;
![\begin{gathered} If: \\ a^b* a^c \\ Then: \\ a^^(b+c) \end{gathered}]()
Applying it to the first two parts of the expression, we will have;
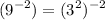
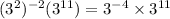
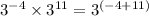

We will also simplify the right side of the expression as follows;
![\begin{gathered} If: \\ \sqrt[a]{b^c} \\ Then: \\ b^{(c)/(a)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ojnuaqsn3dfastksip56bfy8pvzxt5p0t1.png)
![\sqrt[3]{27}=27^{(1)/(3)}](https://img.qammunity.org/2023/formulas/mathematics/college/cnaj7t5x1gupauz39ql5tnxmsv67tljlgn.png)
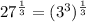
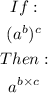
Therefore;
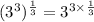
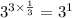
We will now combine all parts of the expression and we'll have;
![(9^(-2))(3^(11))(\sqrt[3]{27})](https://img.qammunity.org/2023/formulas/mathematics/college/grbus0eo7ygl8qxsesh7kqe6s0luttjw0i.png)
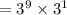

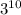
Also we are given the expression:
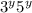
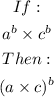
Therefore;

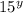
Therefore;
ANSWER: