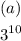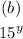Question

a) How would you write `\left(9^{-2}\right)\left(3^{11}\right)\left(\sqrt[3]{27}\right)` as a single pow

Answer 1

Step-by-step explanation:

Given;

We are given the expression shown below;

`(9^(-2))(3^(11))(\sqrt[3]{27})`

Required;

We are required to express this as a single power.

Step-by-step solution;

To do this we would begin by applying some basic rules of exponents;

Applying it to the first two parts of the expression, we will have;

`\begin{gathered} (9^(-2))=(3^2)^(-2) \\ \end{gathered}`
`(3^2)^(-2)(3^(11))=3^(-4)*3^(11)`
`3^(-4)*3^(11)=3^((-4+11))`
`=3^9`

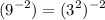
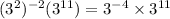
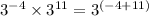
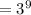
We will also simplify the right side of the expression as follows;

`\begin{gathered} If: \\ \sqrt[a]{b^c} \\ Then: \\ b^{(c)/(a)} \end{gathered}`
`\sqrt[3]{27}=27^{(1)/(3)}`
`27^{(1)/(3)}=(3^3)^{(1)/(3)}`
`\begin{gathered} If: \\ (a^b)^c \\ Then: \\ a^(b* c) \end{gathered}`

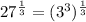
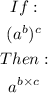
Therefore;

`(3^3)^{(1)/(3)}=3^{3*(1)/(3)}`
`3^{3*(1)/(3)}=3^1`

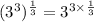
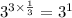
We will now combine all parts of the expression and we'll have;

`(9^(-2))(3^(11))(\sqrt[3]{27})`
`=3^9*3^1`
`=3^(9+1)`
`3^(10)`

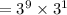
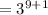
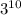
Also we are given the expression:

`3^y5^y`
`\begin{gathered} If: \\ a^b* c^b \\ Then: \\ (a* c)^b \end{gathered}`

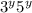
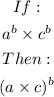
Therefore;

`3^y5^y=(3*5)^y`
`15^y`

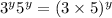
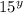
Therefore;

ANSWER:

`\begin{gathered} (a) \\ 3^(10) \end{gathered}`
`\begin{gathered} (b) \\ 15^y \end{gathered}`