The diagram gives a point labelled A, and a line labelled C (with two points marked on it). The distance between two points on a coordinate grid is calculated as follows;
![\begin{gathered} d^2=(x_2-x_1)^2+(y_2-y_1)^2 \\ \text{Hence;} \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o2140v65i7dhafr1dxq6b1yqilecjrkeyo.png)
The variables x and y are as follows;
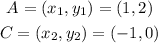
We can now calculate the distance as follows;
![\begin{gathered} d=\sqrt[]{(-1-1)^2+(0-2)^2} \\ d=\sqrt[]{(-2)^2+(-2)^2} \\ d=\sqrt[]{4+4} \\ d=\sqrt[]{8} \\ d=2.8284 \\ d=2.8\text{ units (rounded to the nearest tenth)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rvlzit1h1nmbtus3pwbb71fanav51bvw34.png)
ANSWER:
The distance from point A to line C is therefore 2.8 units (rounded to the nearest tenth)