ANSWER
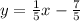
Step-by-step explanation
We want to find the equation of the line that is perpendicular to the given line:
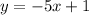
First, we have to find the slope of the line. The slope of a line perpendicular to a given line is the negative inverse of the slope of the line.
The slope of the given line is -5.
Therefore, the slope of the perpendicular line is:
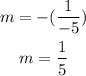
To find the equation of the line, we have to apply the point-slope method:

where (x1, y1) is the point the line passes through.
Therefore, the equation of the line is:

That is the equation of the line.