Question

Six stand-up comics, A, B, C, D, E, and F are to perform on a single evening at a comedy club. The order of performance is determined by random selection. Findthe probability thata. Comic D will perform fourth.b. Comic C-will perform last and Comic B will perform fifthc. The comedians will perform in the following order: D, C, B, A, E, F.d. Comic E or Comic F will perform first.a(Type a fraction Simplify your answer.)(Type a fraction Simplify your answer)c.(Type a fraction. Simplify your answer.)d(Type a fraction Simplify your answer)Time Remaining: 02:00:25NextModule 8 Homework$

Answer 1

a. 1/6

b. 1/30

c. 1/720

d. 1/3

Explanation

a. First, we need to calculate the number of arrangements (like A,B,C,D,E,F; A,C,D,B,F,E, etc.) we can make with six stand-up comics. To calculate this we need to calculate the number of permutations of n = 6 people chosen r = 6 people at a time, as follows:

`\begin{gathered} nPr=(n!)/((n-r)!) \\ _6P_6=(6!)/((6-6)!)=6! \end{gathered}`

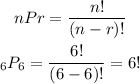
If comic D performs fourth, then we have 5 people (A, B, C, E, and F) and 5 places to order them (1st, 2nd, 3rd, 5th, and 6th). To find the number of ways these arrangements can be made, we need to calculate the number of permutations with n = 5 people chosen r = 5 people at a time, as follows:

`_5P_5=(5!)/((5-5)!)=5!`

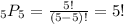
Finally, the probability that Comic D will perform fourth is:

`\begin{gathered} P(\text{ Comic D will perform fourth })=\frac{number\text{ of ways 5 comics can be ordered}}{number\text{ of ways 6 comics can be ordered}} \\ P(\text{ Comic D will perform fourth })=(5!)/(6!) \\ P(\text{ Comic D will perform fourth })=(5!)/(6\cdot5!) \\ P(\text{ Comic D will perform fourth })=(1)/(6) \end{gathered}`

b. If Comic C performs last and Comic B performs fifth, then we need to arrange 4 people in 4 places, that is, we need to calculate the number of permutations with n = 4 people chosen r = 4 people at a time.

`_4P_4=(4!)/((4-4)!)=4!`

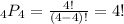
In consequence, the probability that Comic C will perform last and Comic B will perform fifth is:

c. The order: D, C, B, A, E, F is only one of the total possible arrangements. Then, the probability that the comedians will perform in this order is:

`\begin{gathered} P(D,C,B,A,E,F\text{ order})=\frac{number\text{ o fways this order can be made}}{number\text{ of ways 6 com}\imaginaryI\text{cs can be ordered}} \\ P(D,C,B,A,E,F\text{ order})=(1)/(6!) \\ P(D,C,B,A,E,F\text{ order})=(1)/(720) \end{gathered}`

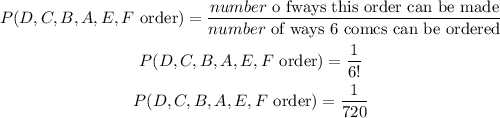
d. The probability that Comic E or Comic F will perform first is computed as follows:

The probability that Comic E (or F) will perform first is numerically equivalent to the probability that Comic D will perform fourth (which was calculated in item a). Therefore,

`\begin{gathered} P(Comic\text{ E will perform first or Comic F will perform first })=(1)/(6)+(1)/(6) \\ P(Com\imaginaryI c\text{ E w}\imaginaryI\text{ll perform f}\imaginaryI\text{rst or Com}\imaginaryI\text{c F w}\imaginaryI\text{ll perform f}\imaginaryI\text{rst})=(2)/(6) \\ P(Com\imaginaryI c\text{ E w}\imaginaryI\text{ll perform f}\imaginaryI\text{rst or Com}\imaginaryI\text{c F w}\imaginaryI\text{ll perform f}\imaginaryI\text{rst})=(1)/(3) \end{gathered}`