This is a geometric sequence problem.
The first term is 10 bacteria cells
and it grows 75% every hour.
It can be represented as :
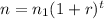
where n is the number of cells after t hours
n1 is the first term
and
r is the growth rate.
Substitute the following values :
n1 = 10
r = 75% or 0.75
t = 1 day which is equal to 24 hrs
The number of cells after 24 hours will be :
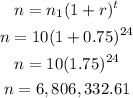
Therefore, the correct answer is Choice C. 6,806,333