Question

A certain bacteria grows 75% every hour. A sick child starts with 10 bacteria cells. How many cells will be in the child’s body at the end of one day? A. 75 B. 75000C. 6,806,333D. -75000

Answer 1

This is a geometric sequence problem.

The first term is 10 bacteria cells

and it grows 75% every hour.

It can be represented as :

`n=n_1(1+r)^t`

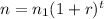
where n is the number of cells after t hours

n1 is the first term

and

r is the growth rate.

Substitute the following values :

n1 = 10

r = 75% or 0.75

t = 1 day which is equal to 24 hrs

The number of cells after 24 hours will be :

`\begin{gathered} n=n_1(1+r)^t_{} \\ n=10(1+0.75)^(24) \\ n=10(1.75)^(24) \\ n=6,806,332.61 \end{gathered}`

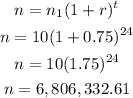
Therefore, the correct answer is Choice C. 6,806,333