Question

State the possible number of positive real zeros,negative real zeros, and imaginary zeros forf(x) = 3x4 – 2x3 – 5x2 + 6x - 2.

Answer 1

Okay, here we have this:

Considering the provided equation, we will identify if its roots are negative, positive or imaginary, so we obtain the following:

`f(x)=3x^4-2x^3-5x^2+6x-2`

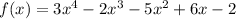
According to the rule of the signs of Descartes, we can identify that since in f(x) there are three changes of signs then there will be 1 or 3 positive roots.

Now, let's find p(-x) to see how many possible negative roots there are:

`\begin{gathered} f(-x)=3\mleft(-x\mright)^4-2\mleft(-x\mright)^3-5\mleft(-x\mright)^2+6\mleft(-x\mright)-2 \\ f(-x)=3x^4+2x^3-5x^2-6x-2 \end{gathered}`

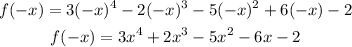
Since there is only one sign change, then there is only one negative root.

Now, finally we will factor it to see how many positive roots we can get:

`\begin{gathered} 3x^4-2x^3-5x^2+6x-2=0 \\ \mleft(x-1\mright)\mleft(3x^3+x^2-4x+2\mright)=0 \end{gathered}`

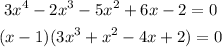
As it cannot be simplified further, we finally obtain that f (x) has a positive root, a negative root and two imaginary ones.