Given:
The number of students like Wolfgang Amadeus Mozart = 36
The number of students like Ludwig von Beethoven = 35
The number of students like Franz Joseph Hayden = 30
The number of students like Mozart and Beethoven = 14
The number of students like Mozart and Hayden = 21.
The number of students like Beethoven and Hayden = 14.
The number of students like all three composers = 9
Required:
We need to draw a ven diagram for the given information.
Step-by-step explanation:
Let M be the set of students that like Mozart, B be the set of students that like Beethoven, and H be the set of students that like Hayden.
a)
We need to find the number of students like exactly two of these composers.
We know that
M and B =14
B and H =14
M and H =21
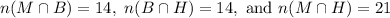
The number of students like exactly two of these composers.
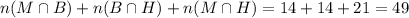
49 students like exactly two of these composers s
b)
We need to find the number of students like exactly one of these composers.
We know that
![n(M)=36,\text{ }n(B)=35,\text{ }n(H)=30,\text{ n}(M\operatorname{\cap}B)=14,\text{ n}(B\operatorname{\cap}H)=14,n(M\operatorname{\cap}H)=21,\text{ and }n(M\cap H\cap B)=9.]()
![n(M\cup B\cup H)=m(M)+\text{ }n(B)+n(H)-n(M\operatorname{\cap}B)-\text{n}(B\operatorname{\cap}H)-n(M\operatorname{\cap}H)+n(M\cap H\cap B)]()
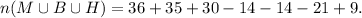
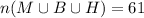
The number of students like the composers =61.
c)
We need to find the number of students who do not like these composers.
We know that
![n(M)=36,\text{ }n(B)=35,\text{ }n(H)=30,\text{ n}(M\operatorname{\cap}B)=14,\text{ n}(B\operatorname{\cap}H)=14,n(M\operatorname{\cap}H)=21,\text{ and }n(M\cap H\cap B)=9.]()
![n(M\cup B\cup H)=m(M)+\text{ }n(B)+n(H)-n(M\operatorname{\cap}B)-\text{n}(B\operatorname{\cap}H)-n(M\operatorname{\cap}H)+n(M\cap H\cap B)]()
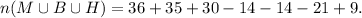
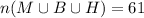
The number of students like the composers =61.
The total number of students = 64
The number of students who do not like composers=64-61 =3
3 students like none of the composers.
d)
We need to find the number of students who like Mozert but neither like Beethoven and Hayden.
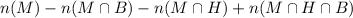
Substitute know values.
![n(M)=36,\text{ n}(M\operatorname{\cap}B)=14,n(M\operatorname{\cap}H)=21,\text{ and }n(M\cap H\cap B)=9.]()
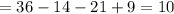
10 students who like Mozert but neither like Beethoven and Hayden.
Final answer:
a) 21
b) 61
c) 3
d) 10