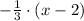Question

Factor -1/3x + 2/3 using the leading coefficient of the variable term

Answer 1

So we have to factor this expression:

`-(1)/(3)x+(2)/(3)`

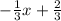
Using the leading coefficient of the variable term. The variable term is that with x and the leading coefficient is the number multiplying the x, in this case:

`-(1)/(3)`

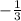
What we are going to do now is take the term that is not the variable term and multiply and divide it by the leading coefficient:

`\begin{gathered} (2)/(3)=(2)/(3)\cdot(-(1)/(3))/(-(1)/(3))=(2)/(3)\cdot(-(1)/(3))\cdot(-(3)/(1))=(2)/(3)\cdot(-3)\cdot(-(1)/(3)) \\ (2)/(3)=(-2)\cdot(-(1)/(3)) \end{gathered}`

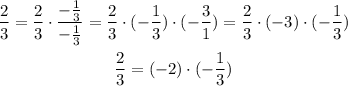
Then we get:

`-(1)/(3)x+(2)/(3)=-(1)/(3)x+(-2)\cdot(-(1)/(3))`

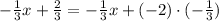
Now that both terms are multiplied by the same number we can factor the expression:

`-(1)/(3)x+(-2)\cdot(-(1)/(3))=-(1)/(3)\cdot(x-2)`

Then the answer is:

`-(1)/(3)\cdot(x-2)`