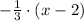So we have to factor this expression:
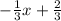
Using the leading coefficient of the variable term. The variable term is that with x and the leading coefficient is the number multiplying the x, in this case:
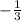
What we are going to do now is take the term that is not the variable term and multiply and divide it by the leading coefficient:
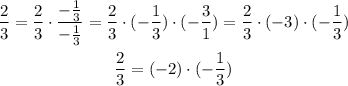
Then we get:
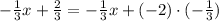
Now that both terms are multiplied by the same number we can factor the expression:

Then the answer is: