To find the mean of departures, we add up all the data and divide by the amount of years, as following:
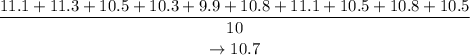
To calculate the median:
1. Organize the data in numerical order:
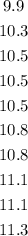
2. Divide the number of data by 2:
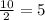
3. Go to the number in that position and average it with the next one to get the median:
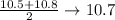
The median is 10.65
The number that appears most often is 10.5
Thereby, the mode is 10.5