Question

Solve the following equation on the interval [0°, 360°), Separate multiple answers with a comma, Remember to include a degree symbol.3sin?x cotx - 3cotr = 0

Answer 1

Given the equation:

`3\sin ^2x\cot x-3\cot x=0`

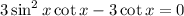
Let's solve the given equation over the interval:

`\lbrack0^o,360^o)`

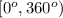
Add 3cotx to both sides of the equation:

`\begin{gathered} 3\sin ^2x\cot x-3\cot x+3\cot x=0+3\cot x \\ \\ 3\sin ^2x\cot x=3\cot x \end{gathered}`

Cancel the common factors:

`3\sin ^2x=3`

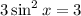
Divide both sides by 3:

`\begin{gathered} (3\sin ^2x)/(3)=(3)/(3) \\ \\ \sin ^2x=1 \end{gathered}`

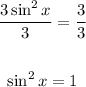
Take the square root of both sides:

`\begin{gathered} \sin x=\sqrt[]{1} \\ \\ \sin x=1 \end{gathered}`

Take the sine inverse of both sides:

`\begin{gathered} x=\sin ^(-1)(1) \\ \\ x=90^o \end{gathered}`

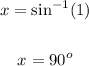
Now, the sine function is positive in quadrant I and II, to find the second solution, add 180 to the reference angle.

x = 90 + 180 = 270 degrees.

Therefore, the solutions to the equation on the given interval:

x = 90⁰, 270⁰

ANSWER:

x = 90⁰, 270⁰