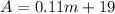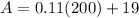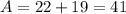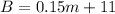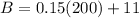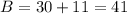Answer:
200 minutes
Explanation:
The first plan:
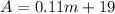
The second plan:
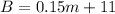
To find the point where the plans are equal in cost, set them equal and solve for
 :
:
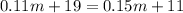
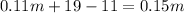
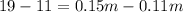
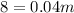
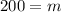
Therefore, at 200 minutes, both calling plans are equal in cost. To verify, we substitute 200 for
 in each formula and check that they are equal:
in each formula and check that they are equal: