Given the ploynomial:
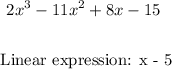
A linear expression (x - n) is a factor of a polynomial when x = n is a zero of the polynomial expression. That is when the function f(x) = 0.
Given the linear expression:
x - 5
Equate to zero:
x - 5 = 0
Add 5 to both sides:
x - 5 + 5 = 0 - 5
x = 5
Substitute 5 for x in the polynomial, if the function tends to zero, then the linear expression is a factor of the polynomial.
We have:

Thus:

Since the the polynomial function f(x) tends to zero, the linear expression can be said to be a factor of the polynomial
ANSWER:
Yes, the linear expression is a factor of the polynomial