Question

determine the length of line AB and line AC in the right triangle. You may give your answer in radical form

Answer 1

Given the right triangle of the figure, we must compute the length of the sides AB and AC.

From the picture we read the following data about the triangle:

- we consider the angle

`\theta=60^(\circ)`

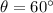
- respect to the angle θ we see that the adjacent cathetus side is BC, and its length is:

`BC=6`

- respect to the angle θ the opposite cathetus is AC

- the hypotenuse of the triangle is AB

We have the following trigonometric identities:

`\begin{gathered} (1)\rightarrow\cos \theta=\frac{\text{adjacent cathetus}}{\text{hypotenuse}} \\ (2)\rightarrow\tan \theta=\frac{\text{opposite cathetus}}{\text{adjacent cathetus}} \end{gathered}`

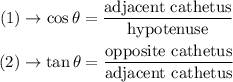
1) Using equation (1) and the data above we compute the value of the hypotenuse AB:

`\begin{gathered} \cos 60^(\circ)=(6)/(AB) \\ AB\cdot\cos 60^(\circ)=6 \\ AB=(6)/(\cos 60^(\circ)) \\ AB=(6)/(0.5)=12 \end{gathered}`

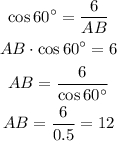
2) Using equation (2) and the data above we compute the value of the opposite cathetus AC:

`\begin{gathered} \tan 60^(\circ)=(AC)/(6) \\ AC=\tan 60^(\circ)\cdot6 \\ AC=\sqrt[]{3}\cdot6 \end{gathered}`

Answers

AB = 12

AC = 6√3