Given:
The population of the bacteria at the beginning = 80
the population grows according to a continuous exponential growth model.
after 14 days, there are 216 bacteria.
y = the number of bacteria after time t
So, the general relation between y and t will be:
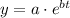
We need to find the values of a and b
At t = 0 y = 80
So,
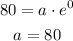
When t = 14 , y = 216
So,
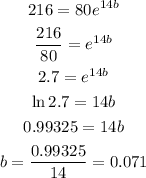
so, the function will be:
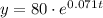
Part b: we need to find the number of bacteria after 23 days
So, substitute with t = 23
so,
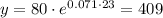
so, after 23 days the number of bacteria = 409