Question

The midpoint of AB is M(0,3). If the coordinates of A are (1,2), what are the coordinates of B?

Answer 1

B(-1,4)

Step-by-step explanation:

Given: The midpoint of AB = M(0,3)

Coordinates of A = (1,2)

We substitute these values into the midpoint formula.

`\begin{gathered} M(x,y)=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ M(0,3)=((1+x_2)/(2),(2+y_2)/(2)) \end{gathered}`

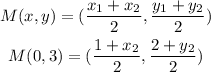
Equating the x-coordinates, we have:

`\begin{gathered} (1+x_2)/(2)=0 \\ 1+x_2=0 \\ x_2=-1 \end{gathered}`

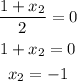
Equating the y-coordinates, we have:

`\begin{gathered} (2+y_2)/(2)=3 \\ 2+y_2=6 \\ y_2=6-2 \\ y_2=4 \end{gathered}`

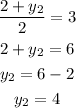
The coordinates of B are (-1,4).