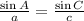EXPLANATION :
From the problem, triangles ADB and CDB are right triangles.
In a right triangle, the sine function is the opposite side divided by the hypotenuse.
Referring to the figure,
sin A = h/c and sin C = h/a which are both definitions of sine ratio.
So the reason is Definition of sine ratio
By multiplication property of equality, use cross multiplication to remove the denominators
That's
c sinA = h
and
a sin C = h
Equating both equations in h :
c sin A = a sin C by the reason of Substitution Property of Equality
Diving both sides by "ac"
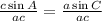
by the reason of Division Property of Equality
Then :