Question

Identify the parametric equations that represent the same graph as the following parametric equations. Select all that apply.x=4ty=t^2-1

Answer 1

Given the equations:

`\begin{gathered} x=4t \\ \\ y=t^2-1 \end{gathered}`

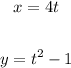
Let's identify the parametric equations which represent the same graph as the given equations.

Here, we have:

Rewrite the first equation for t

`t=(x)/(4)`

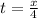
Now, plug in x/4 for t in the second equation:

`\begin{gathered} y=((x)/(4))^2-1 \\ \\ y=(x^2)/(4^2)-1 \\ \\ y=(x^2)/(16)-1 \end{gathered}`

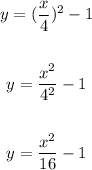
Also we have:

`t^2=(x^2)/(16)`

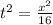
Rewrite equation 2 for t²

`t^2=y+1`

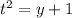
Hence, we have:

`\begin{gathered} (x^2)/(16)=t^2=y+1 \\ \\ (x^2)/(16)=y+1 \\ \\ y=(x^2)/(16)-1 \end{gathered}`

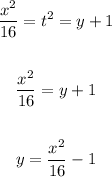
Now, let's solve for the following to confirm:

`\begin{gathered} \text{ When x = 3t} \\ Substitute\text{ 3t for x:} \\ y=((3t)^2)/(16)-1 \\ \\ y=(9t^2)/(16)-1 \\ \end{gathered}`

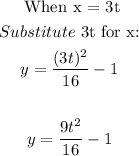
Option B:

`\begin{gathered} \text{ When x = 2t:} \\ \text{ Substitute 2t for x} \\ y=((2t)^2)/(16)-1 \\ \\ y=(4t^2)/(16)-1 \\ \\ y=(t^2)/(4)-1 \\ \\ Option\text{ B is correct.} \end{gathered}`

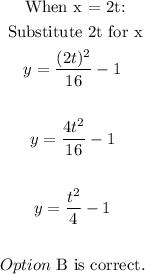
Option C:

`\begin{gathered} \text{ When x =8t} \\ \text{ Substitute 8t for x:} \\ y=((8t)^2)/(16)-1 \\ \\ y=(64t^2)/(16)-1 \\ \\ y=4t^2-1 \\ \\ Option\text{ C is correct.} \end{gathered}`

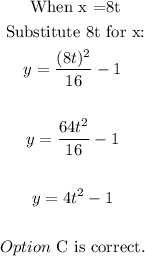
Therefore, the correct parametric equations are:

`\begin{gathered} B.\text{ x = 2t} \\ y=(t^2)/(4)-1 \\ \\ \\ \\ C.x=8t \\ y=4t^2-1 \end{gathered}`

ANSWER:

• B. x = 2t

y = t²/4 - 1

• C. x = 8t

y = 4t² - 1