Given the equations:
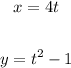
Let's identify the parametric equations which represent the same graph as the given equations.
Here, we have:
Rewrite the first equation for t
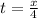
Now, plug in x/4 for t in the second equation:
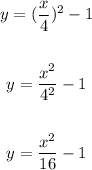
Also we have:
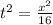
Rewrite equation 2 for t²
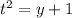
Hence, we have:
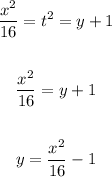
Now, let's solve for the following to confirm:
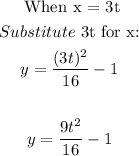
Option B:
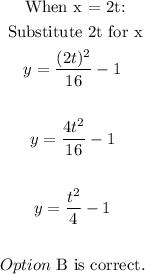
Option C:
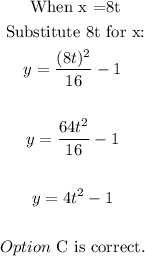
Therefore, the correct parametric equations are:

ANSWER:
• B. x = 2t
y = t²/4 - 1
• C. x = 8t
y = 4t² - 1