Question

Detmermine the best method to solve the following equation, then solve the equation. (3x-5)^2=-125

Answer 1

For the given equation;

`(3x-5)^2=-125`

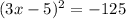
We shall begin by expanding the parenthesis on the left side, after which we would combine all terms on and move all of them to the left side, which shall yield a quadratic equation. Then we shall solve.

Let us begin by expanding the parenthesis;

`\begin{gathered} (3x-5)^2\Rightarrow(3x-5)(3x-5) \\ (3x-5)(3x-5)=9x^2-15x-15x+25 \\ (3x-5)^2=9x^2-30x+25 \end{gathered}`

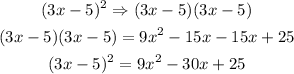
Now that we have expanded the left side of the equation, we would have;

`\begin{gathered} 9x^2-30x+25=-125 \\ \text{Add 125 to both sides and we'll have;} \\ 9x^2-30x+25+125=-125+125 \\ 9x^2-30x+150=0 \end{gathered}`

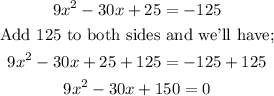
We shall now solve the resulting quadratic equation using the quadratic formula as follows;

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{Where;} \\ a=9,b=-30,c=150 \\ x=\frac{-(-30)\pm\sqrt[]{(-30)^2-4(9)(150)}}{2(9)} \\ x=\frac{30\pm\sqrt[]{900-5400}}{18} \\ x=\frac{30\pm\sqrt[]{-4500}}{18} \\ x=\frac{30\pm\sqrt[]{-900*5}}{18} \\ x=\frac{30\pm\sqrt[]{-900}*\sqrt[]{5}}{18} \\ x=\frac{30\pm30i\sqrt[]{5}}{18} \\ \text{Therefore;} \\ x=\frac{30+30i\sqrt[]{5}}{18},x=\frac{30-30i\sqrt[]{5}}{18} \\ \text{Divide all through by 6, and we'll have;} \\ x=\frac{5+5i\sqrt[]{5}}{3},x=\frac{5-5i\sqrt[]{5}}{3} \end{gathered}`

ANSWER:

`x=\frac{5+5i\sqrt[]{5}}{3},x=\frac{5-5i\sqrt[]{5}}{3}`