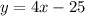Answer:
The equation of the line that is parallel to

and passes through (5,-
Step-by-step explanation:
We want to find the standard form equation of the line that is parallel to

and passes through the points (5, -5)
The equation of the line given above has slope of 4 units, and y-intercept of 2.
Any equation with the slope 4 units and a different y-intercept from 2 - is a parallel line with the line in equation (1).
Let this parallel line be:

Since this line passes through (5, -5), we have x = 5, and y = -5. Substituting these valeus of x and y in equation (2), we can easily find the value of the y-intercept b
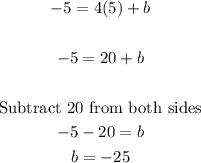
Therefore, the equation of the line is: