We need to calculate the Z-score of the given values.
I'll draw the normal distribution curve for this example
Z-score of 34

If we use a Z table, we can see that a value of Z=-3.615 corresponds to an area of 0.00015
Z-score of 51
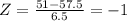
Again, using the Z table, when Z=-1, the area below the curve is 0.15866.
If we substract 0.15866 and 0.00015, we obtain the area between 51 and 34, as shown below
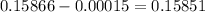
In percentage: 15.851%
Now, let's proceed with 64 and 68
Z-score of 64:
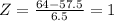
This value represents an area to the left of: 0.84134
Z-score of 68:
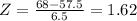
which corresponds to an area to the left of: 0.94738
Again, we must substract those two values to obtain the areal between 68 and 64
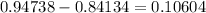
In percentage, this is equal to 10.604%
I will upload an image of Z table in case you want to double check...
Now, in order to conclude the question... we need to check if "68% of the students received scores between 34 or 51 and 64 or 68."
We already know that between 34 and 51 there are 15.851% of students and between 64 and 68 there are 10.604%, which adds a value of 26.455%
In conclusion, the information given is wrong, because it is 26.455% and not 68%