We need to solve the given equation and then find the sum of all possible solutions.
The equation is:
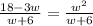
Notice that the denominator on both sides is w+6. Since the denominator can't be zero, we have:
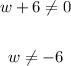
Thus, -6 can't be a solution.
Now, we can solve the equation by rewriting it as
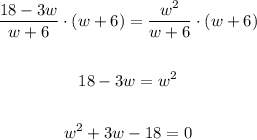
Now, we can use the quadratic formula to solve it:
![\begin{gathered} w=\frac{-3\pm\sqrt[]{3^(2)-4(1)(-18)}}{2(1)} \\ \\ w=\frac{-3\pm\sqrt[]{9+72}}{2} \\ \\ w=\frac{-3\pm\sqrt[]{81}}{2} \\ \\ w=(-3\pm9)/(2) \\ \\ w_1=(-3-9)/(2)=-6\text{ (this solution is not possible)} \\ \\ w_2=(-3+9)/(2)=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bqon746gdj082luk923ft42fvkeeknag07.png)
Therefore, the only possible solution is 3. And the sum of all possible solutions is 3.