hello
the question is a quadratic equation and we are asked to use completing the squares method.
to solve this, let's use some basic steps
step 1
divide through the equation by the coefficient of x^2
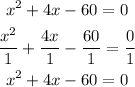
step 2
now we have to know that
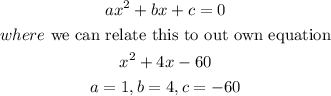
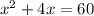
step 3
complete the square on the left hand side of the equation and balance this by adding the same value on the right hand side of the equation
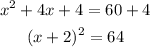
step 4
take the square roots on both sides of the equation
![\begin{gathered} (x+2)^2=64 \\ \sqrt[]{(x+2)^2_{}}=\sqrt[]{64} \\ x+2=\pm8 \\ x=2+8=10 \\ or \\ x=2-8=-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x7ju2vzlnad0zlju4mzxdytflfqnv75jv0.png)
from the calculations above, the value of x is either 10 or -8