Question

Solve the equation for all values of x by completing the square x^2+4x-60=0

Answer 1

hello

the question is a quadratic equation and we are asked to use completing the squares method.

to solve this, let's use some basic steps

step 1

divide through the equation by the coefficient of x^2

`\begin{gathered} x^2+4x-60=0 \\ (x^2)/(1)+(4x)/(1)-(60)/(1)=(0)/(1) \\ x^2+4x-60=0 \end{gathered}`

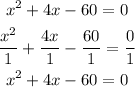
step 2

now we have to know that

`\begin{gathered} ax^2+bx+c=0 \\ where\text{ we can relate this to out own equation} \\ x^2+4x-60 \\ a=1,b=4,c=-60 \end{gathered}`
`x^2+4x=60`

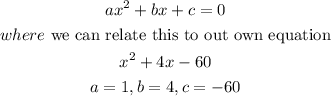
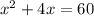
step 3

complete the square on the left hand side of the equation and balance this by adding the same value on the right hand side of the equation

`\begin{gathered} x^2+4x+4=60+4 \\ (x+2)^2=64 \end{gathered}`

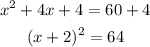
step 4

take the square roots on both sides of the equation

`\begin{gathered} (x+2)^2=64 \\ \sqrt[]{(x+2)^2_{}}=\sqrt[]{64} \\ x+2=\pm8 \\ x=2+8=10 \\ or \\ x=2-8=-6 \end{gathered}`

from the calculations above, the value of x is either 10 or -8